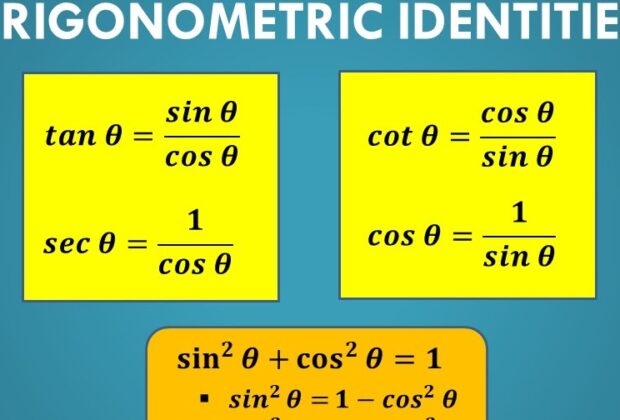
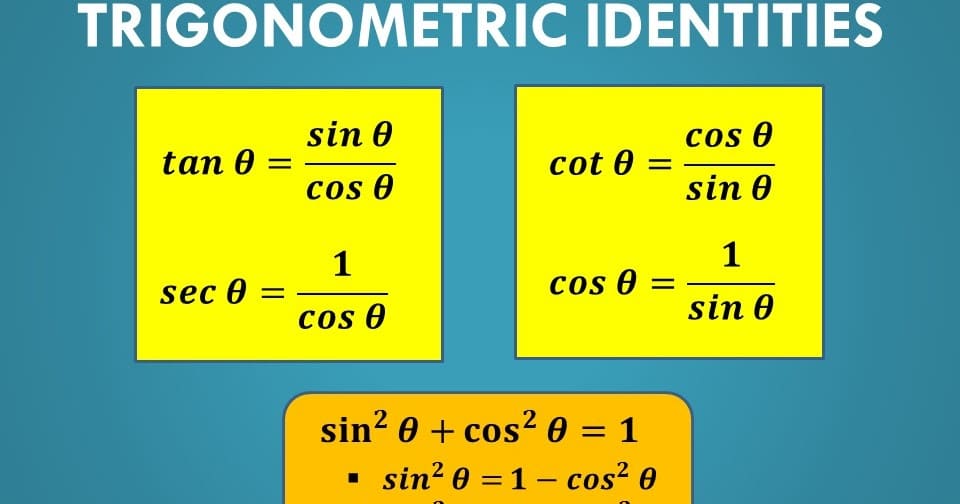
As trigonometric functions are used in an expression or an equation, identities come in handy. Identity inequalities are inequalities that hold any value on both sides of any given equation. These identities are geometrically defined as functions of one or more angles. The side length, as well as the angle of a triangle, have many different identities. Sine, cosine, tangent, cosecant, secant, and cotangent are the six fundamental and essential trigonometric ratios. The sides of the right triangle, such as the adjacent, opposite, and hypotenuse sides, are used to describe all of these trigonometric ratios. The six trigonometric ratios are the source of all fundamental trigonometric identities. Let’s look at the list of trigonometry identities, how they are derived, and how it’s used.
Trigonometric Identities and their Laws
The Law of Sines
The law of sines states that it can be used to find unknown angles and sides in any triangle.
Solving Triangles Using The Law of Sines: The estimates of the angles and sides of right triangles were found using trigonometry in previous concepts. We’ll now look at the law of sines, which helps us to solve for any triangle’s angles and side lengths. Any other triangle is an oblique triangle, while a right triangle has a 90-degree angle. Finding the measurements of all three angles is needed to solve an oblique triangle.
The Law of Cosines
The law of cosines states that it can be used to solve for angles and sides of a triangle in cases where other laws do not apply or fit in.
Using The Law of Cosines
In some instances, we may not have exact and accurate information to apply the Law of Sines to find unknown angles and sides in a triangle. For instance, consider a triangle where all the three sides are known and with their positions, but no angle values are given to be exact. In such scenarios, there is not enough information to use the Law of Sines.
The Law of Cosines is beneficial for:
- Computing the third side of a triangle when two sides and their enclosed angle are recognized and given, and
- Computing the angles of a triangle if only the three sides are known with their respective positions.
What is the Pythagoras Theorem?
The square of the hypotenuse side of a right-angled triangle is equal to the number of squares of the other two sides, according to Pythagoras’ theorem. Perpendicular, Base, and Hypotenuse are the names of the triangle’s three sides. Since it is opposite the angle of 90°, the hypotenuse is the longest side. When s is positive, the sides of a right triangle (say, a, b, and c) have positive integer values.
Pythagoras Theorem Formula:
Imagine a triangle given in this instance: Where “a” is the perpendicular of the triangle, “B” here is the base, and “c” is the hypotenuse. According to the above definition, the Pythagoras theorem formula is stated as:
- Hypotenuse² = Perpendicular² + Base²
- c² = a² + b²
Applications of Pythagoras Theorem
The application of the theorem is stated below:
- To prove and state if the triangle is a right-angled triangle or not.
- In a right-angled triangle, calculate the length of any side of the triangle if the other two sides are given.
- The theorem is also applicable to squares when we have to find the diagonal of a square.
When is the Theorem used?
Pythagoras theorem is useful and beneficial to find the sides of a right-angled triangle. If we know any two sides of a right triangle, then we can find the third side of the triangle with its value.
Conclusion
Trigonometric identities are very well discussed and explained on Cuemath which is an online learning platform. This platform has a wide range of diverse examples that connect mathematics to the student’s day-to-day activity.




Leave a Reply